psu-matematicas: guauuuuuu !!!! de fmat tomado! (falta sólo una pregunta)

martes, 11 de diciembre de 2012

guauuuuuu !!!! de fmat tomado! (falta sólo una pregunta)

Conjuntos numéricos, Proporcionalidad, Álgebra y Funciones

1: -3 - (-7)*5
R: 32

2: El valor de 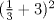$TEX: $ (\frac{1}{3} + 3)^2 $$ es:
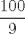
R: $TEX: $\displaystyle \frac{100}{9}$$

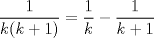3: $TEX: $\displaystyle \frac{1}{k(k+1)} = \frac{1}{k} - \frac{1}{k+1} $$ . La suma de los primeros 99 términos es:
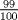
R: $TEX: $ \frac{99}{100} $$

4: Si al triple del sucesor de un número no es menor ni igual que el doble del cuadrado del doble del número, la expresión que lo representa es:
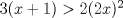
R: $TEX: $ 3(x+1) > 2(2x)^2 $$

5: 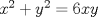$TEX: $ x^2 + y^2 = 6xy $$ , con x > y. ¿Cuál es el valor de 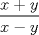$TEX: $ \displaystyle \frac{x+y}{x-y} $$ ?
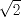
R: $TEX: $ \sqrt{2} $$

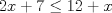
6: Cual de los siguientes conjuntos contiene elementos del conjunto solución de la inecuación $TEX: $2x + 7 \le 12 + x$$

I) Los numeros reales menores a 5.
II) Los numeros reales mayores a 5.
III) Un conjunto formado solo por el 5.
R: I y III

7: ¿Por cual número se debe multiplicar 0,01 para obtener la unidad?
R: 100

8: Sea 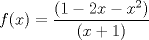$TEX: $\displaystyle f(x) = \frac{(1-2x-x^2)}{(x+1)}$$ , el valor de 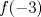$TEX: $f(-3)$$ es:
R: 1

9: Si 3,6x=36 y 4,8*100=w ¿Cuánto vale xw?
R: 4800

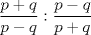
10: ¿Cuál es el valor de $TEX: $\displaystyle \frac{p+q}{p-q}:\frac{p-q}{p+q}$$
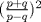
R: $TEX: $ (\frac{p+q}{p-q})^2$$

11: Se tiene un número de 4 dígitos tal que dos de sus dígitos son iguales. Uno de los dígitos distintos es igual al otro más cinco. El otro dígito distinto es igual a un tercio del dígito que se repite. ¿Cuál de los siguientes números corresponde a esta definición?

I) 3316
II) no me acuerdo, pero no era
III) 9389
R: I y III

12: En una micro van 30 personas sentadas, ocupando cada uno 1 asiento y no quedando más asientos disponibles, por lo que van 10 personas paradas. Pero en el siguiente paradero se bajan el 20% de las personas sentadas y el 30% de las personas paradas y en ese mismo paradero se suben 2 personas. Si ocupan un asiento por persona, no dejando más disponibles ¿Cuántas personas quedan paradas al final?
R: 3

13: Se compran 5 artículos a $300 cada uno. Si esto equivale a 3M, ¿Cuál es el valor de m?
R: $500

14: Carlos tiene $x pesos. Su amiga tiene 30 veces más que el doble de lo que tiene Carlos. ¿Cuanto dinero tiene la amiga de Carlos?
R: $TEX: $2x + 30$$

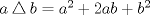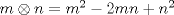15: Si definimos $TEX: $ a \bigtriangleup b = a^2 + 2ab + b^2 $$ y $TEX: $ m \otimes n = m^2 - 2mn + n^2 $$ , entonces $TEX: $ 4 \otimes 3 - 5 \bigtriangleup 3 $$ es
R: -63

16: La razón entre dos números es 2:3 y la diferencia entre ellos es 45, ¿Cuánto vale el menor de los números?
R: 90

17: Se tienen tres números en razón 3:5:7 y cuya suma vale 45. Éstos números son:
R: 9, 15, 21

18: Cual de las siguientes afirmaciones es verdadera:
R: $TEX: $ \sqrt{ \sqrt[3]{4} } = \sqrt[3]{2} $$

19: Por cuanto se debe multiplicar 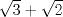$TEX: $ \sqrt{3} + \sqrt{2}$$ para obtener un número racional:

I) $TEX: $ 2\sqrt{3} - 2\sqrt{2} $$
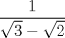
II) $TEX: $ \displaystyle \frac{1}{\sqrt{3} - \sqrt{2}} $$
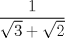
III) $TEX: $ \displaystyle \frac{1}{\sqrt{3} + \sqrt{2}} $$
R: I y III

20: De las siguientes afirmaciones, son verdaderas:

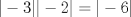
I) $TEX: $|-3||-2| = |-6|$$
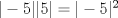
II) $TEX: $ |-5||5| = |-5|^2$$
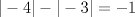
III) $TEX: $|-4|-|-3| = -1$$
R: I y II

21: La recta 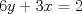$TEX: $6y + 3x = 2$$ corta al eje de las abscisas en:
R: $TEX: $\displaystyle \frac{2}{3}$$

22: Si el a% del 5% de b es igual a c, y el %b del 10% de c es a, entonces la relación entre a y c es:
R: $TEX: $ a^2 = 2c^2 $$

23: Si incialmente había un capital de 800.000 y al cabo de un tiempo t se tiene el doble de dicho capital con un interés compuesto anual del 5% ¿Cuál es el valor de t?
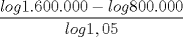
R: $TEX: $\displaystyle \frac{log1.600.000 - log800.000}{log1,05} $$

24: ¿Cuales de los siguientes datos representan una proporcionalidad directa?
R1: La tabla con valores 1 y 3, 2 y 6, 3 y 9

25: Cual de las siguientes afirmaciones son SIEMPRE verdades (n entero):

I) 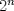$TEX: $2^n$$ es divisible por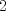 $TEX: $2$$
II) 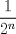$TEX: $\displaystyle \frac{1}{2^n}$$ es menor que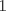 $TEX: $1$$
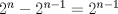
III) $TEX: $2^n - 2^{n-1} = 2^{n-1}$$
R: Sólo III

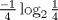
26: El valor de $TEX: $ \frac{-1}{4} \log_{2}{\frac{1}{4}} $$
R: $TEX: $ \frac{1}{2} $$

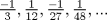
27: La expresión que representa a la sucesión de núemros: $TEX: $ \frac{-1}{3}, \frac{1}{12}, \frac{-1}{27}, \frac{1}{48}, ... $$
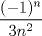
R: $TEX: $\displaystyle \frac{(-1)^n}{3n^2}$$

28: Si un grupo que incialmente tiene 200 personas y al cabo de cada semana duplica su valor, la función que representa dicha relación es:
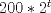
R: $TEX: $200*2^t$$

29: Se tiene un segmento APB tal que AP mide 36 y AB es a PB como 7 es a 3. ¿Cuánto mide PB?
R: 27

30: ¿Cuál de las siguientes funciones puede representar el gráfico de la figura?

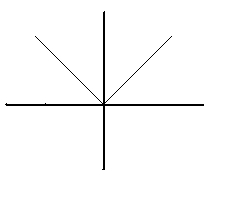
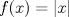
I) $TEX: $ f(x) = |x| $$
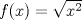
II) $TEX: $ f(x) = \sqrt{x^2} $$
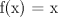
III) $TEX: f(x) = x$
R: I y II

31: Sea 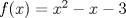$TEX: $f(x) = x^2-x-3$$ , el valor de 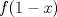$TEX: $f(1-x)$$ es:
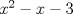
R: $TEX: $x^2-x-3$$

32: De las siguientes afirmaciones, es(son) verdadera(s) (con x real positivo):

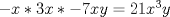
I) $TEX: $-x*3x*-7xy = 21x^3y$$
II) $TEX: $????$$
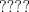
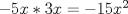
III) $TEX: $-5x*3x = -15x^2$$
R: I y III (no me acuerdo del orden, la cuestión es que eran dos verdaderas)

33: Del sistema de ecuaciones:
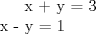
$TEX: <br />x + y = 3 \\<br />x - y = 1 \\<br />$

Es correcto afirmar que:

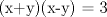
I) $TEX: (x+y)(x-y) = 3$
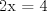
II) $TEX: 2x = 4$
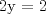
III) $TEX: 2y = 2$
R: I, II y III

34: ¿Cual de los siguientes gráficos podría representar a la función ax-3?

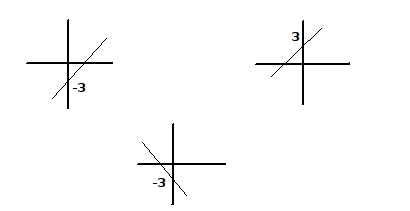
R: Los dos gráficos que cortan al eje Y en -3.

35: Sea 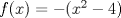$TEX: $f(x) = -(x^2-4)$$ , cual de las siguiente afirmaciones es FALSA:
R: La función corta al eje de las ordenadas en el punto (0, -4).

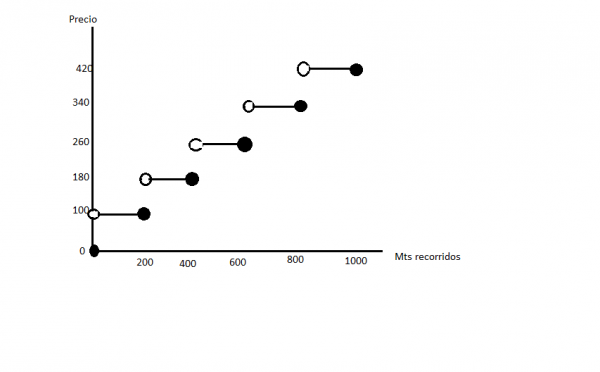
36: Una tarifa de un taxi tiene un costo fijo de $100, más un costo adicional de $80 por cada 200 metros recorridos o fracción. ¿Cuál de los siguientes gráficos representa mejor la situación anterior?
R:

37: Sea 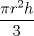$TEX: $\displaystyle \frac{\pi r^2h}{3}$$ la fórmula para calcular el volumen de una pirámide. ¿Cuál de las siguientes afirmaciones es (son) cierta(s)?

I) Si el radio aumenta el doble, el volumen aumenta el doble.
II) Si el radio aumenta el cuádruple, el volumen aumenta a la mitad.
III) Si el radio aumenta el doble y el volumen se mantiene constante, la altura se divide por cuatro.
R: Sólo III.

Geometría y Trigonometría

38: Cual de las siguientes afirmaciones es falsa:
R: Las diagonales de un trapecio isósceles son ejes de simetría

39: Se tiene un cuadrado PQRS y se le aplican rotaciones y traslaciones ¿Cuál de los siguientes gráficos NO pudo
haber sido generado?
R: Aquél en donde P y Q eran vértices opuestos.

40: ¿Con cual de las siguientes alternativas por separado se puede teselar la figura completamente?

R: Sólo II o III

41: Se tiene una circunferencia P de centro (-7,-1) y otra Q de centro (-5,2). Si se trasladó P hasta Q ¿Cuál era el vector traslación?
R: (2,3)

42: Dados los vectores a y b (no me acuerdo de los valores), calcular el valor de 4a-2b.
R: (9, 36)

43: Cual de las siguientes ternas no es un trio pitagorico:
R: 12, 16, 24

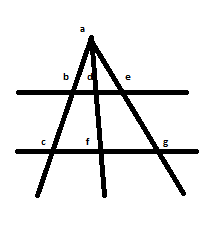
44: Según la figura, cual de las siguientes proporciones es correcta:
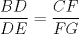
R: $TEX: $\displaystyle \frac{BD}{DE} = \frac{CF}{FG}$$

45: En la figura, el punto A tiene coordenadas (0,1,0), el punto B (1,0,0) y el punto C (0,0,1). Al respecto, cual de las siguientes afirmaciones es verdadera:

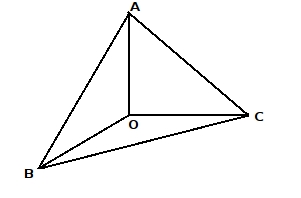
I) El plano AOB es perpendicular al plano AOC
II) El plano ABO es perpendicular al plano ABC
III) El plano OBC es perpendicular al pano AOC
R: I y III

46: Un niño cuya mano se encuentra a 1m. del suelo eleva un volantín con una elevación de 60 grados como se muestra en la figura. ¿Cual es el valor de h?

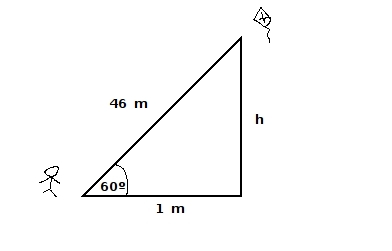
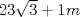
R: $TEX: $ 23\sqrt{3} +1 m$$

47: En la figura, OB = BD y AB es diámetro. ¿Cuál es el valor del ángulo CDA?

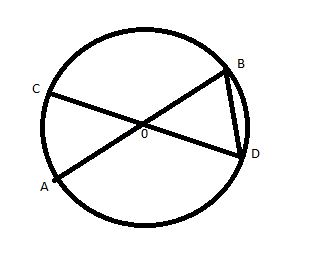
R: 30

48: En la figura el triángulo ABC es equilátero y BQ es a QC como 1 es a 2. Además, CD y AQ se cruzan en E, ¿Cuál es la razón entre los triángulos AED y ABC?

R: $TEX: $ \frac{1}{10} $$

49: ¿Cuál de las siguientes figura representa triángulos semejantes?

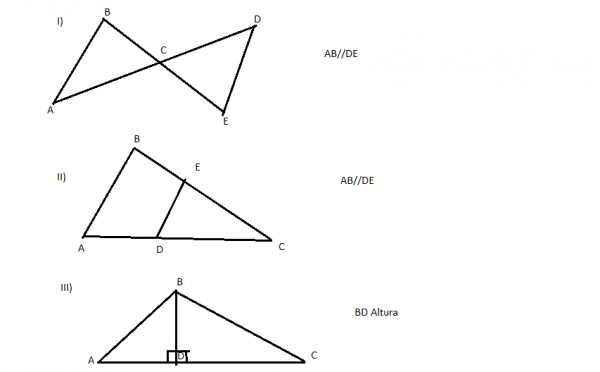
I) ABC ~ DEC
II) CAB ~ CDE
III) ACB ~ BAD
R1: I y II

50: En la figura, el triángulo PQR es congruente con el triángulo STU.

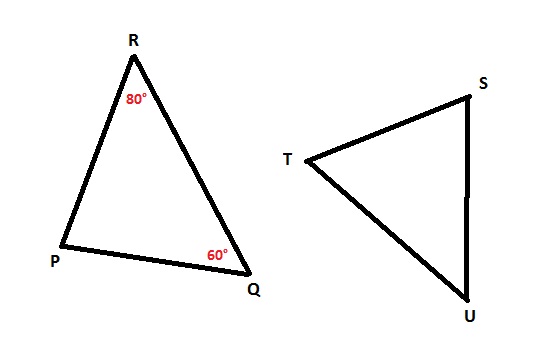
De las siguientes afirmaciones, son verdaderas:

I) Ángulo TSU = 40º
II) Ángulo PQ = Ángulo ST
III) TS > PQ
R: I y II

51: En la figura, el triángulo ABC es congruente con el triángulo DEF. Se tiene que AC = BC y FG es altura del triángulo DEF.

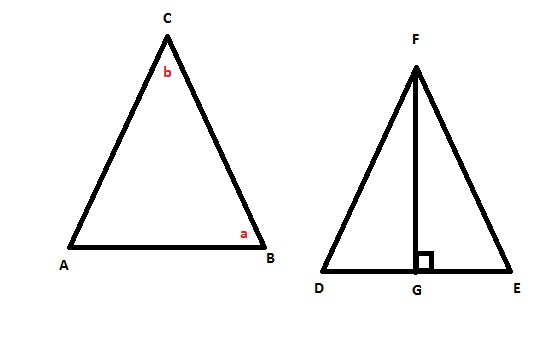
Al respecto, es cierto que:

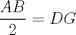
I) $TEX: $\displaystyle \frac{AB}{2} = DG$$
II) $TEX: $DGF = EGF$$
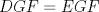
III) ABC puede ser equilatero
R: mini-polémica: I y II - I, II y III

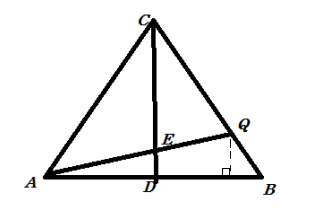
52: En la figura, ABC es rectángulo en B, DB es altura y E es punto medio de AC. Calcular el valor del segmento DE.

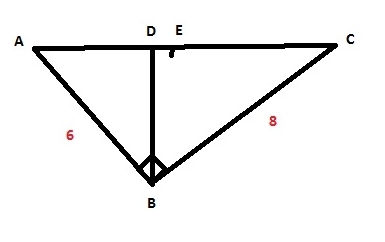
R: 1,4

53: ¿Cuantros triángulos como el de la figura son necesarios para teselar un rombo de lado 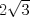$TEX: $2\sqrt{3}$$ y ángulo interior 60º?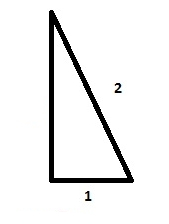

R: 12

54: En la circunferencia de centro O mostrada en la figura, ¿Cuál es valor que SIEMPRE representa a a en función de b?

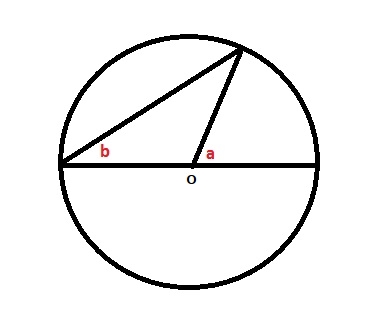
R: a = 2b

55: ¿Cuánto vale el coseno del ángulo a?

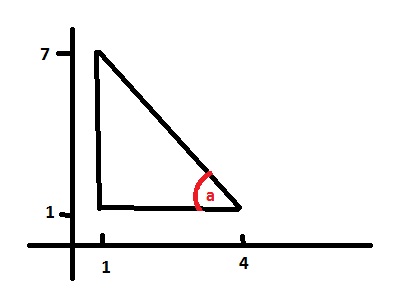
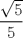
R: $TEX: $ \displaystyle \frac{\sqrt{5}}{5} $$

56: ¿Cuál es el valor de x en la figura?

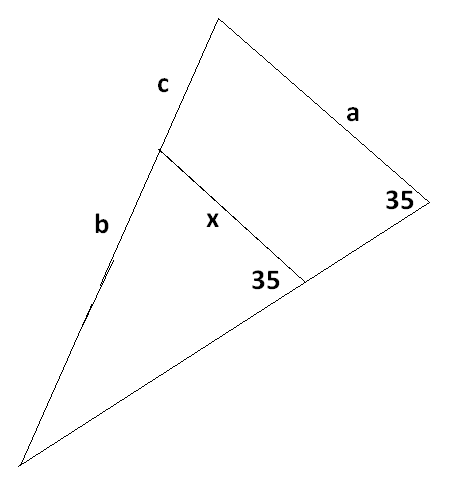
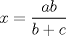
R: $TEX: $\displaystyle x=\frac{ab}{b+c}$$

Estadística y Probabilidad

57: Tabla con sucesos A1 hasta A8. Una vez completado los datos de frecuencia acumulada y relativa pedían calcular la probabilidad que ocurriera A6 ó A8.
R: 0,3

58: Tabla con consumo eléctrico según meses. De lo que me acuerdo:

Mayo -> 370
Junio -> 430
Julio -> 490
Agosto -> 310
Septiembre -> 380
Octubre -> 320
Noviembre -> 320

Al respecto, son verdaderas:

I) La mayor variación de consumo fue entre Agosto y Septiembre.
II) El valor absoluto de la variación entre Junio y Julio fue igual a la variación entre Mayo y Junio.
III) En Noviembre no hubo consumo.
R: I y II

59: Muestran una tabla con valores, frecuencias acumuladas y relativas. En base a dicha tabla ¿Qué gráfico puede ser construido?

I) Gráfico de Valores v/s Frecuencia
II) Gráfico de torta con porcentajes (frecuencias relativas)
III) Gráfico de %Frecuencia v/s Valores
Mini-polémica: I y II - I, II y III

60: Se tiene una lista de valores (creo que era 1,3,3,3,4,5,5,6,6), al cambiar un 6 por un 7 cambia:

I) La moda
II) La media aritmética
III) La mediana
R: Sólo II

61: Había una tabla con valores y preguntaba por el percentil 50.
R: 4

62: Se tienen 3 monedas. Se define la variable aleatoria p como la probabilidad que salgan 0 caras y se define la variable aleatoria q como la probabilidad que salgan 2 caras. ¿Cuál es el valor de p+q?
R: $TEX: $ \frac{1}{2} $$

63: En un estante se tienen 6 vestidos. ¿De cuántas maneras se pueden escoger 2 vestides de dicho estante?
R: 15

64: Se tiene una bolsa con 48 bolas del mismo tipo, la mitad de ellas son blancas y la otra mitad rojas. Si se saca de la bolsa la mitad de las blancas y un tercio de las rojas, ¿cuál es la probabilidad de sacar una bola roja?
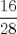
R: $TEX: $\displaystyle \frac{16}{28}$$

65: Se tienen 13 libros en una biblioteca, de los cuales 8 son de matemática. De estos 8 libros, la mitad son rojos. ¿Cuál es la probabilidad de sacar un libro de matemática y que además sea rojo?
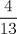
R: $TEX: $\displaystyle \frac{4}{13}$$

66: Se tienen dos urnas con bolas iguales. En la primera hay 3 blancas y 4 rojas. En la segunda hay 5 blancas y 7 rojas. Si se extrae una bola de cada urna, ¿Cuál es la probabilidad de que ambas sean blancas?
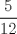
R: $TEX: $\displaystyle \frac{3}{7}$$ x $TEX: $\displaystyle \frac{5}{12}$$

67: En un experimento se lanza una moneda. Si sale cara, se vuelve a lazar la moneda y si sale cruz se lanza un dado. ¿Cuál es la probabilidad de lanzar el dado?
R: $TEX: $\displaystyle \frac{1}{2}$$

Suficiencia de datos

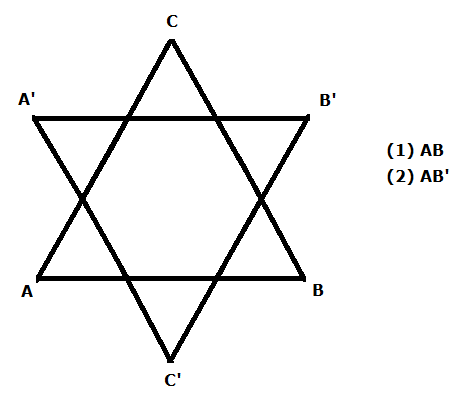
68: Respecto de la figura, se puede saber el área del hexágono regular si se sabe:

1) El valor de AB
2) El valor de A'B
R: Cada una por sí sola

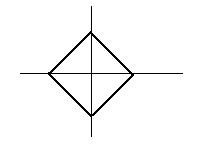
69: Se tiene un rombo como el de la figura y se hace girar en torno al eje Y. Se puede calcular el volumen
del cuerpo generado si:
1) Sabemos el valor de uno de los lados del rombo
2) Sabemos el valor de la diagonal principal
R: Ambas juntas

70: Sean 3 hermanos de distintas edades. Se puede determinar la edad del hermano mayor si:

1) La media aritmética es 25.
2) La mediana es 23
R: Se require información adicional.

71: Sea 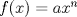$TEX: $ f(x) = ax^n $$ . Se puede saber el valor de a y n si:

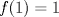
1) $TEX: $ f(1) = 1 $$
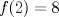
2) $TEX: $ f(2) = 8 $$
R: Ambas juntas

72: Sean m y n enteros positivos. Se puede determinar que m es mayor que n si:

1) m+n = 13
2) m-n = 3
R: Sólo (2) por sí sola

73: Se puede comprobar que p es un número (entero?) par si:

I) 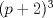$TEX: $ (p+2)^3 $$ es par.
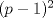II) $TEX: $ (p-1)^2 $$ es impar.
R: Polémico: Ambas juntas, Cada una por separado, Se requiere información adicional

74: Se puede determinar que a+b es múltipo de 9 si:

1) a es múltiplo de 4 y b es múltiplo de 5
2) a-b es múltiplo de 9
R: Se requiere información adicional