viernes, 30 de agosto de 2013
Desafío - Suficiencia de Información (Resuelto)
Respuesta:
Veamos Sólo (1)
Si son enteros consecutivos, entonces: (x+(x+1)+(x+2)+(x+3)+(x+4))/5, no es spoble de conocerse puesto que no sabemos el valor de x.
Veamos Sólo (2)
Si sabemos que la mediana es 20, pero sin saber otro dato, como el que sean consecutivos, no se puede saber el promedio. Veamos dos ejemplos que nos lleven a dos promedio distintos, aunque sepamos la mediana: a) 1,1,20,30,30; y b) 4,4,20,21,21 .... sabiendo la mediana "20", no podemos saber el promedio ....
Pero con (1) y (2) ..... sabemos que la mediana (x+2) = 20, de donde x=18 y luego tenemos el promedio.
(1) y (2), ambas juntas. Alternativa C)
Fuente: UFSM
NEM: Primero Medio.
Eje Temático: IV.) Datos y Azar.
CMO: Estadígrafos.
Desafío - Regularidad Algebraica (Resuelto)
Respuesta: La secuencia es, pensando que el término PRIMERO es = x, es:
0) 0x-0
1) 1x+0 = x (Primer Término)
3) 2x-1
4) 3x+1
5) 4x-2
6) 5x+2
7) 6x-3
8) 7x+3
Luego el séptimo y octavo suman: (6x-3) + (7x+3) = 13x
Alternativa A)
Fuente: UFSM
NEM: Primero Medio.
Eje Temático: II.) Álgebra.
CMO: Regularidad Algebraica.
Etiquetas:
1ro. Medio,
Buscar un Término,
Regularidad Algebraica
Desafío - Funciones (Resuelto)
Respuesta:
f(-1) = (-5)^2 = (-5)(-5) = 25
f(0) = (0)^2 = (0)(0) = 0
f(12) = 12-10 = 2
f(-1)+f(0)-f(12) = 25 + 0 - 2 = 23
Alternativa C)
Fuente: UFSM
NEM: Segundo Medio.
Eje Temático: II.) Álgebra.
CMO: Funciones.
Desafío - Volumen (Resuelto)
Respuesta:
Por proporciones continuas y si llamamos x, y, z a las aritas del paralelepípedo, tendremos:
x/12=y/3=z/4 = k
luego
x=12k
y=3k
z=4k
(Estas correspondencias las reemplazaremos al interior de la raíz que ahora viene)
Sabemos que la diagonal de un paralelepípedo es:
luego: x=24 ; y=6 ; z= 8
Luego la superficie es
2(24x6 + 24x8 + 6x8) = 768
Alternativa C)
Fuente: UFSM
NEM: Cuarto Medio.
Eje Temático: III.) Geometría.
CMO: Proporciones Continuas. Volumen.
Etiquetas:
4to. Medio,
Aristas,
Diagonal,
Proporción Continua,
Volumen
Desafío - Exponenciales (Resuelto)
Respuesta:
Alternativa B)
Fuente: Ensayo PSU Universidad Federico Santa María (UFSM)
NEM: Segundo Medio.
Eje Temático: II.) Álgebra.
CMO: Exponenciales.
Etiquetas:
2do. Medio,
Despejar una Expresión,
Exponenciales,
Propiedades Potencias
martes, 27 de agosto de 2013
Desafío - Problema de Planteo (Resuelto)
La fábrica de Pablo hizo 4250 barras de chocolate. Había tres tipos de chocolate: Blanco, Negro y chocolate con leche. La cantidad de barras de chocolate blanco era 715 más que la cantidad de barras de chocolate con leche. La cantidad de barras de chocolate negro era 5 veces la cantidad de barras de chocolate con leche. ¿Cuántas barras de chocolate negro se hicieron en la fábrica?
A) 3535
B) 505
C) 2525
D) 1220
E) Ninguna de las anteriores.
Respuesta:
LLamemos B al chocolate Blanco, N al chocolate Negro, Ch al chocolate con leche.
i) B + N + Ch = 4250
ii) N = 5Ch
iii) B = Ch + 715
Podemos poner ii) y iii) en i) para así dejar una única ecuación en términos de Ch
(Ch + 715) + 5Ch + Ch = 4250
Ch + 5Ch + Ch + 715 = 4250
7Ch = 4250 - 715
Ch = 3535/7 = 505
Luego reemplazamos en ii)
N = 5Ch = 5(505) = 2525
Alternativa C)
Fuente: Método Singapur 4to. Básico
NEM: Primero Medio.
Eje Temático: II.) Álgebra.
CMO: Planteo de ecuaciones.
A) 3535
B) 505
C) 2525
D) 1220
E) Ninguna de las anteriores.
Respuesta:
LLamemos B al chocolate Blanco, N al chocolate Negro, Ch al chocolate con leche.
i) B + N + Ch = 4250
ii) N = 5Ch
iii) B = Ch + 715
Podemos poner ii) y iii) en i) para así dejar una única ecuación en términos de Ch
(Ch + 715) + 5Ch + Ch = 4250
Ch + 5Ch + Ch + 715 = 4250
7Ch = 4250 - 715
Ch = 3535/7 = 505
Luego reemplazamos en ii)
N = 5Ch = 5(505) = 2525
Alternativa C)
Fuente: Método Singapur 4to. Básico
NEM: Primero Medio.
Eje Temático: II.) Álgebra.
CMO: Planteo de ecuaciones.
Etiquetas:
1ro. Medio,
Planteo de Ecuaciones,
Problema de Planteo
lunes, 26 de agosto de 2013
Desafío - Tabla (Resuelto)
Respuesta: Veamos una a una las proposiciones:
I) Veamos las variaciones de los meses contiguos, en valor absoluto una a una:
mayo junio = 60
junio julio = 60
julio agosto = 30
agosto septiembre = 70
septiembre octubre = 10
octubre noviembre = 0
Verdadera!
II) del listado anterior, ambas valen 60. Verdadera!
III) SÍ lo hubo, 320. Falsa!
Sólo I y II son verdaderas, Alternativa B)
Fuente: DEMRE 2012
NEM: Primero Medio.
Eje Temático: IV.) Datos y Azar.
CMO: Interpretación de Tabla.
Etiquetas:
1ro. Medio,
Datos y Azar,
Interpretación Tabla,
Tabla
domingo, 25 de agosto de 2013
Desafío - Geometría (Resuelto)
Respuesta:
Alternativa A)
Fuente: PreU.P.Valdivia-Específica.
NEM: Primero Medio.
Eje Temático: III.) Geometría.
CMO: Elementos Secundarios en el Triángulo.
viernes, 23 de agosto de 2013
Desafío - Técnicas de Conteo (Resuelto)
Un conjunto A posee "n" elementos, siendo n mayor que 4. El número de subconjuntos de A con cuatro elementos es:
Respuesta:
Puesto que dos conjuntos que tienen los mismos elementos, en diferente orden, son iguales, estamos en presencia de una combinación. Son las combinaciones C(n,4). Acá n debe ser mayor que 4 para poder elegir varios conjuntos, en el borde, cando n=4, se puede escoger un sólo conjunto.
C(n,4) = { n! } / (4! x (n-4)! } , pero 4! = 4x3x2x1 = 24
Luego la respuesta, tal como sale en la pregunta es: n!/(24x(n-4)!)
Alternativa E)
Fuente: PreU.P.Valdivia-Específica
NEM: Primero Medio.
Eje Temático: IV.) Datos y Azar.
CMO: Técnicas de Coneto.
Respuesta:
Puesto que dos conjuntos que tienen los mismos elementos, en diferente orden, son iguales, estamos en presencia de una combinación. Son las combinaciones C(n,4). Acá n debe ser mayor que 4 para poder elegir varios conjuntos, en el borde, cando n=4, se puede escoger un sólo conjunto.
C(n,4) = { n! } / (4! x (n-4)! } , pero 4! = 4x3x2x1 = 24
Luego la respuesta, tal como sale en la pregunta es: n!/(24x(n-4)!)
Alternativa E)
Fuente: PreU.P.Valdivia-Específica
NEM: Primero Medio.
Eje Temático: IV.) Datos y Azar.
CMO: Técnicas de Coneto.
Etiquetas:
1ro. Medio,
Combinatoria,
Números Combinatorios,
Técnicas de Conteo
Desafío - Técnicas de Conteo (Resuelto)
¿De cuántas maneras se puede escoger dos personas del mismo sexo entre 5 varones y 7 damas?
Respuesta:
La posibilidad de elegir 2 varones entre los 5, pues no importa el orden en que son elegidos es C(5,2).
La posibilidad de elegir 2 mujeres entre 7, pues no importa el orden en que son elegidos es C(7,2).
Luego por el principio de la suma, las posibilidades totales son: C(5,2) + C(7,2).
Con otra escritura .... La respuesta correcta es la alternativa C)
Fuente: PreU.P.Valdivia-Específica
NEM: Primero Medio.
Eje Temático: IV.) Datos y Azar.
CMO: Técnicas de Coneto.
Respuesta:
La posibilidad de elegir 2 varones entre los 5, pues no importa el orden en que son elegidos es C(5,2).
La posibilidad de elegir 2 mujeres entre 7, pues no importa el orden en que son elegidos es C(7,2).
Luego por el principio de la suma, las posibilidades totales son: C(5,2) + C(7,2).
Con otra escritura .... La respuesta correcta es la alternativa C)
Fuente: PreU.P.Valdivia-Específica
NEM: Primero Medio.
Eje Temático: IV.) Datos y Azar.
CMO: Técnicas de Coneto.
Etiquetas:
1ro. Medio,
Combinatoria,
Técnicas de Conteo
Desafío - Técnicas de Conteo (Resuelto)
¿Cuántas "palabras" (con o sin sentido) que NO empiecen por consonante se pueden formar revolviendo las letras de la palabra PEDRO?
A) 12
B) 24
C) 48
D) 60
E) 120
Respuesta: Pensemos que queremos llenar 5 espacios ( ) ( ) ( ) ( ) ( )
con las letras de PEDRO, y con las restricciones que nos imponen.
Tenemos que en el primer casillero sólo pueden ir las letras: E, O, pues no debe empezar con consonante.
(2) x ( ) x ( ) x ( ) x ( )
en el segundo casillero pueden algunas de las 4 letras restantes,
en el tercero algunas de las 3 restantes
en el segundo alguna de las 2 restantes
y en él último la letra que quede .... Luego por el principio multiplicativo tenemos
(2) x (4) x (3) x (2) x (1) = 2 x 4! = 2 x 24 = 48
Alternativa C)
Fuente: PreU.P.Valdivia-Específica
NEM: Primero Medio.
Eje Temático: IV.) Datos y Azar.
CMO: Técnicas de Coneto.
A) 12
B) 24
C) 48
D) 60
E) 120
Respuesta: Pensemos que queremos llenar 5 espacios ( ) ( ) ( ) ( ) ( )
con las letras de PEDRO, y con las restricciones que nos imponen.
Tenemos que en el primer casillero sólo pueden ir las letras: E, O, pues no debe empezar con consonante.
(2) x ( ) x ( ) x ( ) x ( )
en el segundo casillero pueden algunas de las 4 letras restantes,
en el tercero algunas de las 3 restantes
en el segundo alguna de las 2 restantes
y en él último la letra que quede .... Luego por el principio multiplicativo tenemos
(2) x (4) x (3) x (2) x (1) = 2 x 4! = 2 x 24 = 48
Alternativa C)
Fuente: PreU.P.Valdivia-Específica
NEM: Primero Medio.
Eje Temático: IV.) Datos y Azar.
CMO: Técnicas de Coneto.
Desafío - Técnicas de Conteo (Resuelto)
En una elección, 8 candidatos postulan a 3 cargos DIFERENTES. ¿Cuál es el numero de resultados distintos que pueden producirse?
A) 10
B) 60
C) 56
D) 336
E) Ninguno de los anteriores.
Respuesta:
En este caso, si importa el orden, porque los cargos son diferentes, es decir, si los cargos son presidente, secretario y tesorero, no da lo mismo que Juan sea tesorero y María presidenta que todo al revés .... Por tanto no estamos en presencia de una combinación sino de una variacion de 8 sobre 3.
Respuesta: V(8,3) = 8!/(8-3)! = 8!/5! = (8x7x6x5)!/5! = 8x7x6= 336 : Alternativa D)
Fuente: PreU.P.Valdivia-Específica.
NEM: Primero Medio.
Eje Temático: IV.) Datos y Azar.
CMO: Técnicas de Conteo.
A) 10
B) 60
C) 56
D) 336
E) Ninguno de los anteriores.
Respuesta:
En este caso, si importa el orden, porque los cargos son diferentes, es decir, si los cargos son presidente, secretario y tesorero, no da lo mismo que Juan sea tesorero y María presidenta que todo al revés .... Por tanto no estamos en presencia de una combinación sino de una variacion de 8 sobre 3.
Respuesta: V(8,3) = 8!/(8-3)! = 8!/5! = (8x7x6x5)!/5! = 8x7x6= 336 : Alternativa D)
Fuente: PreU.P.Valdivia-Específica.
NEM: Primero Medio.
Eje Temático: IV.) Datos y Azar.
CMO: Técnicas de Conteo.
Etiquetas:
1ro. Medio,
Técnicas de Conteo,
Variaciones
Desafío - Técnicas de Conteo (Resuelto)
En un barco se dispone de 5 banderas diferentes. ¿Cuántas señales se puede enviar izando tres banderas en un mástil?
A) 5
B) 10
C) 15
D) 30
E) 60
Respuesta: En este caso importa el orden y como se deben disponer 3 banderas de un total mayor igual a 5, acá estamos en presencia de Variaciones.
Son Variaciones de (5,3) = { 5! / (5-3)! } = (5x4x3x2!)/(2!) = 60
Alternativa E)
Fuente: PreU.P.Valdivia-Específica
NEM: Primero Medio.
Eje Temático: IV.) Datos y Azar.
CMO: Técnicas de Conteo.
A) 5
B) 10
C) 15
D) 30
E) 60
Respuesta: En este caso importa el orden y como se deben disponer 3 banderas de un total mayor igual a 5, acá estamos en presencia de Variaciones.
Son Variaciones de (5,3) = { 5! / (5-3)! } = (5x4x3x2!)/(2!) = 60
Alternativa E)
Fuente: PreU.P.Valdivia-Específica
NEM: Primero Medio.
Eje Temático: IV.) Datos y Azar.
CMO: Técnicas de Conteo.
Etiquetas:
1ro. Medio,
Técnicas de Conteo,
Variaciones
Desafío - Técnicas de Conteo (Resuelto)
¿De cuántas maneras diferentes puede un cliente ordenar un "sandwich" y una bebida si hay cinco clases de "sandwiches" y cuatro bebidas en el menú?
A) P(5,4)
B) C(5,4)
C) 9
D) 20
E) Ninguna de las anteriores.
Respuesta:
Alternativa D)
Fuente: PreU.P.Valdivia-Específica
NEM: Primero Medio.
Eje Temático: IV.) Datos y Azar.
CMO: Técnicas de Conteo.
A) P(5,4)
B) C(5,4)
C) 9
D) 20
E) Ninguna de las anteriores.
Respuesta:
Alternativa D)
Fuente: PreU.P.Valdivia-Específica
NEM: Primero Medio.
Eje Temático: IV.) Datos y Azar.
CMO: Técnicas de Conteo.
Etiquetas:
1ro. Medio,
Principio Multiplicativo,
Técnicas de Conteo
lunes, 19 de agosto de 2013
Desafío - Congruencia (Resuelto)
 |
| http://psu-matemticas.blogspot.com |
Respuesta:
Entonces es la Alternativa C)
Fuente: Santillana-1ro. Medio
NEM: Primero Medio.
Eje Temático: III.) Geometría.
CMO: Congruencia.
Etiquetas:
1ro. Medio,
Angulos Congruentes,
Congruencia,
Rectángulo,
Triángulo,
Triángulos Congruentes
domingo, 18 de agosto de 2013
Desafío - Uno con Raíces (Resuelto)
Respuesta:
La idea es elevar al cuadrado, y tener ojo que en el término de la izquierda habrá un cuadrado de binomio.
Por otra parte, el cuadrado de una raíz cuadrada nos deja solita la cantidad subradical, entonces:
Alternativa A)
Fuente: PreU.P.Valdivia.
NEM: Segundo Medio.
Eje Temático: II.) Álgebra.
CMO: Raíces. Productos Notables.
Desafío - Volumen (Resuelto)
El rectángulo ABCD tiene un perímetro de 14 cm. Su lado menor mide 2 cm. Si este rectángulo se hace girar en torno a uno de sus largos, el volumen en centímetros cúbicos es:
A) 10 Pi
B) 20 Pi
C) 25 Pi
D) 28 Pi
E) Ninguna de las anteriores.
Respuesta:
Entonces el ancho mide 2 cm, el largo mide "L":
2x2 + 2xL = 14
2L = 14 - 4 = 10
L = 10/2 = 5 cm
Volumen:
Alternativa B)
Fuente: PreU.P.Valdivia.
NEM: Cuarto Medio.
Eje Temático: III.) Geometría.
CMO: Volumen en rotación.
A) 10 Pi
B) 20 Pi
C) 25 Pi
D) 28 Pi
E) Ninguna de las anteriores.
Respuesta:
Entonces el ancho mide 2 cm, el largo mide "L":
2x2 + 2xL = 14
2L = 14 - 4 = 10
L = 10/2 = 5 cm
Volumen:
Alternativa B)
Fuente: PreU.P.Valdivia.
NEM: Cuarto Medio.
Eje Temático: III.) Geometría.
CMO: Volumen en rotación.
Etiquetas:
4to. Medio,
Perímetro Rectángulo,
Rectángulo,
Volumen,
Volumen en Rotación
Desafío - Trigonometría (Resuelto)
Respuesta:
La suma del seno al cuadrado de un ángulo más el coseno al cuadrado del mismo ángulo es una identidad trigonométrica de valor igual a 1, independiente del ángulo.
En este caso el ángulo es dos veces alfa, da lo mismo cual sea el ángulo.
Alternativa A)
Fuente: PreU.P.Valdivia.
NEM: Tercero Medio.
Eje Temático: III.) Geometría.
CMO: Trigonometría. Identidades Trigonométricas-
Etiquetas:
3ro.Medio,
Geometría,
Identidad Trigonométrica,
Trigonometría
Desafío - Potencias (Resuelto)
Respuesta:
Alternativa D)
Fuente: PreU.P.Valdivia.
NEM: Primero Medio.
Eje Temático: I.) Números.
CMO: Potencias.
Desafío - Potencias (Resuelto)
Respuesta:
Alternativa A)
Fuente: PREU.P.Valdivia
NEM: Primero Medio
Eje Temático: II.) Álgebra.
CMO: Potencias.
Etiquetas:
1ro. Medio,
Potencias,
Simplificación,
Suma de Potencias
Desafío - Números (Resuelto)
Si m y n son números enteros positivos y (m+n) es par, ¿Cuál(es) de las siguientes expresiones representa(n) siempre un número par?
I) 2n + m
II) mn
III) m-n
A) Sólo I
B) Sólo II
C) Sólo III
D) Sólo II y III
E) I, II, III
Respuesta:
I) Sea n=1; m=3, luego (m+n)=1+3=4 es par, pero 2n + m = 2+3 = 5: NO ES PAR.
II) Sea n=1, m=3, luego n+m=4; pero mn = 3: NO ES PAR.
III) SIEMPRE es par .... pensemos: n=2p+1; m= 2q+1, ambos son impares por definición, luego al restarlos, se elimina el 1 y queda: (2p - 2q) ó (2q - 2p) que es par, SIEMPRE!
Alternativa C)
Fuente: PreU.P.Valdivia.
NEM: Primero Medio.
Eje Temático: I.) Números.
CMO: Números. Números Pares e Impares.
I) 2n + m
II) mn
III) m-n
A) Sólo I
B) Sólo II
C) Sólo III
D) Sólo II y III
E) I, II, III
Respuesta:
I) Sea n=1; m=3, luego (m+n)=1+3=4 es par, pero 2n + m = 2+3 = 5: NO ES PAR.
II) Sea n=1, m=3, luego n+m=4; pero mn = 3: NO ES PAR.
III) SIEMPRE es par .... pensemos: n=2p+1; m= 2q+1, ambos son impares por definición, luego al restarlos, se elimina el 1 y queda: (2p - 2q) ó (2q - 2p) que es par, SIEMPRE!
Alternativa C)
Fuente: PreU.P.Valdivia.
NEM: Primero Medio.
Eje Temático: I.) Números.
CMO: Números. Números Pares e Impares.
Etiquetas:
1ro. Medio,
Número Impar,
Número Par,
Números
jueves, 15 de agosto de 2013
Desafío - Sistema Inecuaciones (Resuelto)
¿Cuántos números enteros cumplen simultáneamente con las dos condiciones siguientes?
I) El triple del número no suera la mitad, aumentada en 5 unidades.
II) El exceso del cuádruplo del número sobre 2 supera las 6 unidades.
A) 6
B) 7
C) 8
D) 9
E) 10
Respuesta:
Fuente: PreU.P.Valdivia.
NEM: Cuarto Medio.
Eje Temático: II.) Álgebra.
CMO: Sistema de Inecuaciones.
I) El triple del número no suera la mitad, aumentada en 5 unidades.
II) El exceso del cuádruplo del número sobre 2 supera las 6 unidades.
A) 6
B) 7
C) 8
D) 9
E) 10
Respuesta:
Fuente: PreU.P.Valdivia.
NEM: Cuarto Medio.
Eje Temático: II.) Álgebra.
CMO: Sistema de Inecuaciones.
lunes, 12 de agosto de 2013
Desafío - División Algebraica (Resuelto)
Respuesta:
Usemos la División Sintética:
Alternativa C)
Fuente: PSU-Matemáticas-UC Libro Ejercicios
NEM: Primero Medio.
Eje Temático: II.) Álgebra.
CMO: División Polinomios. División Algebraica. División Sintética.
Etiquetas:
1ro. Medio,
Algebra,
División Algebraica,
División de Polinomios,
División Sintética
miércoles, 7 de agosto de 2013
Desafío - Ecuación (Resuelto)
Respuesta: Desarrollamos este ejercicio en el ámbito de los números Reales:
Alternativa -1
Fuente: PSU-U.Católica-Cuaderno de Ejercicios
NEM: Segundo Medio.
Eje Temático: II.) Álgebra.
CMO: Ecuaciones con Radicales.
Etiquetas:
2do. Medio,
Ecuación con Radicales,
Raíces,
Raíces Cúbicas
Desafío - Bicuadrática (Resuelto)
Respuesta:
Fuente: PSU-U.Católica-Cuaderno de Ejercicios
NEM: Tercero Medio.
Eje Temático: II.) Álgebra.
CMO: Ecuación BI-Cuadrática.
Desafío - Cuadrática (Resuelto)
Respuesta:
a=1
b=k
c=36
Para que la solución sea un sólo punto (o que ambas soluciones sean iguales), el discriminante debe ser cero:
k^2 - 4(1)(36) = 0
k^2 = 144
k = +12 ; k = -12
Alternativa D)
Fuente: PSU-U.Católica-Cuaderno de Ejercicios
NEM: Tercero Medio.
Eje Temático: II.) Álgebra.
CMO: Ecuación Cuadrática.
Desafío - Ecuación con Valor Absoluto (Resuelto)
Respuesta:
Si yo sustituyo en x, dentro del valor absoluto como lo indica la ecuación, los valores de -12 y 12, en ambos casos se va a cumplir la ecuación, por tanto las raíces son -12 y 12, Alternativa B)
Fuente: PSU-U.Católica-Cuaderno de Ejercicios
NEM:
Eje Temático:
CMO:
Desafío - Suma de Raíces (Resuelto)
Respuesta:
Alternativa D)
Fuente: PSU-U.Católica-Cuaderno de Ejercicios
NEM: Segundo Medio.
Eje Temático: 1.) Números.
CMO: Raíces.
Desafío - Inecuación (Resuelto)
Respuesta:
Fuente: PSU-U.Católica-Cuaderno de Ejercicios
NEM: Cuarto Medio.
Eje Temático: I.) Álgebra.
CMO: Inecuaciones.
lunes, 5 de agosto de 2013
Desafío - Irracional (Resuelto)
Respuesta:
A) Esta es la correcta .... la expresión equivale a: 0,7071067 ..... de infinitas cifras decimales que NO poseen periodo.
B) Es negativo, por ello se descarta, pues debe estar entre 0 y 1, y esto sucede porque raíz de (3) es mayor que raíz de (2).
C) 1/7 NO es irracional, es racional, tiene la forma de fracción y toda fracción es racional.
D) 0,5 NO es irracional = 1/2.
E) 0,9999....... = 1, NO es irracional.
Fuente: PreU.U.Católica.
NEM: Primero Medio.
Eje Temático: I.) Números.
CMO: Conjuntos Numéricos.
Etiquetas:
1ro. Medio,
Conjuntos Numéricos,
Números Irracionales,
Raíces Inexactas
Desafío - Irracionales (Resuelto)
Respuesta:
 |
| http://psu-matematicas.blogspot.com |
Sólo II) ---- Alternativa B)
Fuente: PreU.U.Católica.
NEM: Primero Medio.
Eje Temático: I.) Números.
CMO: Conjuntos Numéricos.
Etiquetas:
1ro. Medio,
Conjuntos Numéricos,
Números Irracionales,
Raíces Inexactas
Desafío - Fracciones (Resuelto)
25/3
A) 8
B) 8,3
C) 8,33
D) 8,333
E) Ocho enteros un tercio.
Respuesta:
3 cabe 8 veces exactas en 25 y sobre 1/3
Alternativa E)
Fuente: PreU.U.Católica.
NEM: Primero Medio.
Eje Temático: I.) Números.
CMO: Conversión de Fracción Impropia a Número Mixto.
A) 8
B) 8,3
C) 8,33
D) 8,333
E) Ocho enteros un tercio.
Respuesta:
3 cabe 8 veces exactas en 25 y sobre 1/3
Alternativa E)
Fuente: PreU.U.Católica.
NEM: Primero Medio.
Eje Temático: I.) Números.
CMO: Conversión de Fracción Impropia a Número Mixto.
Desafío - Longitud de Trazo (Resuelto)
Respuesta:
Fuente: PreU.U.Católica.
NEM: Tercero Medio.
Eje Temático: III.)Geometría.
CMO: Teorema de Pitágoras.
Etiquetas:
3ro.Medio,
Ecuación,
Teorema Particular de Pitágoras,
Triángulo Rectángulo
Desafío - Longitud de Trazo (Resuelto)
Respuesta:
Alternativa C)
Fuente: PreU.U.Católica.
NEM: Tercero Medio.
Eje Temático: III.) Geometría.
CMO: Triángulo Rectángulo. Trigonometría.
Suscribirse a:
Comentarios (Atom)














.bmp)



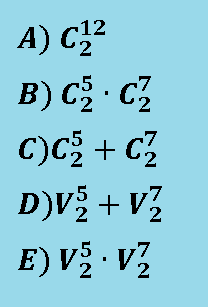






















.bmp)

























