Si x + 2 = y, entonces:
A) - 4
B) -2
C) 0
D) 2
E) 4
Respuesta:
Alternativa E)
Fuente: PSU-3ro. EducaUC
NEM: Segundo Medio.
Eje Temático: I. Álgebra y Funciones.
CMO: Función Valor Absoluto
miércoles, 25 de abril de 2012
Desafío - Muestras
 |
| Hacer click en la imagen para agrandar |
Por todas las anteriores, alternativa E)
Para saber un gusto alimenticio NO es necesario entrevistar a toda la población.
Otras veces, para medir la resistencia de un elemento, debiéndo ser golpeado e inutilizado, es mejor probar sólo una muestra de ellos.
Indagar una población entere es muy costoso económicamente y requiere de largo tiempo, una muestra soluciona estos dos aspectos ...
Fuente: Creación personal.
NEM: Cuarto Medio.
Eje Temático: III Probabilidad y Estadística.
CMO: Estadísticas. población y Muestra.
lunes, 23 de abril de 2012
Noticia de Ensayos ....
USM y Educarchile:
Esta semana parten ensayos para la PSU
Esta semana parten ensayos para la PSU
Para apoyar a quienes rendirán la PSU este año, la Universidad Federico Santa María y Educarchile comenzarán esta semana con ensayos de este test . La USM programó pruebas, en todos sus campus y sedes, para este 28 de abril, el 2 de junio y el 6 de octubre. El 10 de noviembre desarrollará un ensayo final para quienes obtuvieron los mejores puntajes. Hay que inscribirse en www.ensayopsu.cl. En tanto, el portal educarchile.cl tendrá un ensayo online el 25, 26 y 27 de abril. El puntaje se entregará apenas termine la prueba.
Desafío - Isometría
Respuesta:
Entonces, quedamos con la Alternativa C)
Fuente: Material P. Valdivia.
NEM: Primero Medio.
Eje Temático: III. Geometría.
CMO: Isometrías.
Entonces, quedamos con la Alternativa C)
Fuente: Material P. Valdivia.
NEM: Primero Medio.
Eje Temático: III. Geometría.
CMO: Isometrías.
viernes, 20 de abril de 2012
Desafío - Angulos dentro de la Circunferencia
Respuesta:
Alternativa C)
Fuente: Texto 2do. Eduardo Cid
NEM: Segundo Medio.
Eje Temático: II Geometría.
CMO: Ángulo del Centro y Ángulo Inscrito.
Alternativa C)
Fuente: Texto 2do. Eduardo Cid
NEM: Segundo Medio.
Eje Temático: II Geometría.
CMO: Ángulo del Centro y Ángulo Inscrito.
jueves, 19 de abril de 2012
Desafío - Lenguaje Algebraico
 |
| Hacer Click en la imagen para agrandar |
Veamos una a una las proposiciones:
I) VERDADERA:
Área achurada = (c)(c) + a(b - c) = (c)(c) + (a)(b) - (a)(c)
lo que es igual a { ab - c( a-c) }
II) VERDADERA: ABCD es un rectángulo (o cuadrado).
Área ABCD = (CD)(CB) = (b)(a+c)
lo cual es igual a { b(c+a) }
III) FALSA:
Area BGIF es (b)(c) - (c)(c)
y NO al revés, hay una diferencia de SIGNO solamente.
Alternativa B)
Fuente: material PreU. P. Valdivia.
NEM: Primero Medio.
Eje Temático: II. Álgebra y Funciones.
CMO: Lenguaje Algebraico.
Desafío - Lenguaje Algebraico
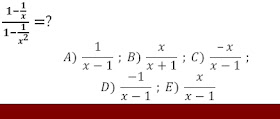 |
| hacer doble click para agrandar |
Alternativa B)
Fuente: material PreU. P. Valdivia.
NEM: Primero Medio.
Eje Temático: II. Álgebra y Funciones.
CMO: Lenguaje Algebraico.
miércoles, 18 de abril de 2012
Desafío - Ecuaciones Exponenciales
Respuesta:
Alternativa D)
Fuente: Recopilación A. Sánchez.
NEM: Cuarto Medio.
Eje Temático: I. Álgebra y Funciones.
CMO: Ecuaciones Exponenciales.
Alternativa D)
Fuente: Recopilación A. Sánchez.
NEM: Cuarto Medio.
Eje Temático: I. Álgebra y Funciones.
CMO: Ecuaciones Exponenciales.
martes, 17 de abril de 2012
Desafío - Geometría
Respuesta:
Alternativa E)
Fuente: Geometría Arrayán
NEM: Primero Medio.
Eje Temático: III. Geometría.
CMO: Geometría Básica.
Alternativa E)
Fuente: Geometría Arrayán
NEM: Primero Medio.
Eje Temático: III. Geometría.
CMO: Geometría Básica.
lunes, 16 de abril de 2012
Desafío - Productos Notables
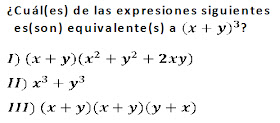 |
| http://psu-matematicas.blogspot.com |
B) Sólo II
C) Sólo III
D) Sólo I y II
E) Sólo I y III
Respuesta: Revisemos cada una de las expresiones:
I) VERDADERA, porque el trinomio corresponde al cuadrado de (x+y), que multiplicado por el binomio (x+y) nos lleva a el cubo de (x+y).
II) FALSA, acá se muestran dos términos (los cubos de x e y) que son sólo una parte del desarrollo del cubo del binomio.
III) VERDADERA, si ordenamos el tercer paréntesis tendremos que (x+y)(x+y)(x+y) es igual al cubo de (x+y)
Alternativa E)
Fuente: Libro de Ejercicios PSU - U.Católica.
NEM: Primero Medio.
Eje Temático: II) Álgebra y Funciones
CMO: Productos Notables
Desafío - Conjuntos Numéricos
Respuesta:
Desarrollemos el cuadrado de binomio, para ello puedes ver primero el link: Cuadrado de Binomio
Fuente: Libro de Ejercicios PSU - U.Católica.
NEM: Primero Medio.
Eje Temático: I) Números y Proporcionalidad.
CMO: Conjuntos Numéricos.
Desarrollemos el cuadrado de binomio, para ello puedes ver primero el link: Cuadrado de Binomio
Fuente: Libro de Ejercicios PSU - U.Católica.
NEM: Primero Medio.
Eje Temático: I) Números y Proporcionalidad.
CMO: Conjuntos Numéricos.
domingo, 15 de abril de 2012
Desafío - Funciones
En la imagen van entrando insumos "x" .... y cada uno de ellos es procesado primero a g(x) y este resultado luego es procesado a f(g(x)) ...
Respuesta: Efectivamente lo que se está mostrando es la composición de funciones: fog(x)=f(g(x)).
Alternativa C)
Fuente: Creación Personal.
NEM: Segundo Medio.
Eje Temático: I. Álgebra y Funciones.
CMO: Funciones
Respuesta: Efectivamente lo que se está mostrando es la composición de funciones: fog(x)=f(g(x)).
Alternativa C)
Fuente: Creación Personal.
NEM: Segundo Medio.
Eje Temático: I. Álgebra y Funciones.
CMO: Funciones
viernes, 13 de abril de 2012
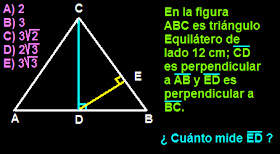
Desafío - Geometría
Nota: Este ejercicio es de un poco mayor dificultad que los que aparecen habitualmente en la PSU.
Respuesta: Completamos los lados de la figura y los ángulos:
Nos quedamos con el triángulo ACD:
Acá usamos el Teorema del SENO:
Introducimos los valores y trabajamos:
Seguimos Trabajando la Expresión:
Para finalmente llegar a:
Fuente: Recopilación Pedro Campillai
NEM: Tercero Medio.
Eje Temático: II. Geometría.
CMO: Ley del Seno. Tangente del ángulo Medio.
Desafío - Función por Tramos
Respuesta:
Alternativa D)
Fuente; PSU U. Católica - Guía de Ejercicios
NEM: Segundo Medio.
Eje Temático: I. Álgebra y Funciones.
CMO: Funciones. Función por Tramos.
Alternativa D)
Fuente; PSU U. Católica - Guía de Ejercicios
NEM: Segundo Medio.
Eje Temático: I. Álgebra y Funciones.
CMO: Funciones. Función por Tramos.
jueves, 12 de abril de 2012
Desafío - Ángulos
Respuesta:
La suma de los ángulos internos de un triángulo completan 180º, entonces:
(x) + (110 - x) + (x + 10) = 180º
Sumando entonces:
x + 120 = 180
x = 180 - 120
x = 60
110 - x = 110 - 60 = 50 ; Alternativa A)
Fuente: PUC . manual de Preparación PAA - Matemáticas (1997)
NEM: Primero Medio.
Eje Temático: III. Geometría.
CMO: Geometría Básica. Angulos.
La suma de los ángulos internos de un triángulo completan 180º, entonces:
(x) + (110 - x) + (x + 10) = 180º
Sumando entonces:
x + 120 = 180
x = 180 - 120
x = 60
110 - x = 110 - 60 = 50 ; Alternativa A)
Fuente: PUC . manual de Preparación PAA - Matemáticas (1997)
NEM: Primero Medio.
Eje Temático: III. Geometría.
CMO: Geometría Básica. Angulos.
miércoles, 11 de abril de 2012
Desafío - Funciones
Respuesta:
El denominador será conflictivo si se hace igual a "0", y ello ocurre cuando x = 2, solamente.
Alternativa D)
Fuente: Libro de Ejercicios PSU - U. Católica.
NEM: Segundo Medio.
Eje Temático: I) Álgebra y Funciones.
CMO: Funciones.
El denominador será conflictivo si se hace igual a "0", y ello ocurre cuando x = 2, solamente.
Alternativa D)
Fuente: Libro de Ejercicios PSU - U. Católica.
NEM: Segundo Medio.
Eje Temático: I) Álgebra y Funciones.
CMO: Funciones.
martes, 10 de abril de 2012
Desafío - Funciones
Alternativa C)
Fuente: Libro de Ejercicios PSU - U. Católica.
NEM: Segundo Medio.
Eje Temático: I) Álgebra y Funciones.
CMO: Funciones.
Desafío - Funciones
Respuesta:
Mirar el Link: Prueba de la Recta Vertical
Fuente: Creación Personal
NEM: Segundo Medio.
Eje Temático: I) Álgebra y Funciones.
CMO: Funciones. Prueba de la Recta Vertical.
Mirar el Link: Prueba de la Recta Vertical
Fuente: Creación Personal
NEM: Segundo Medio.
Eje Temático: I) Álgebra y Funciones.
CMO: Funciones. Prueba de la Recta Vertical.
lunes, 9 de abril de 2012
Desafío - Volumen Cilindro
Fuente: Guía CEPECH
NEM: Cuarto Medio.
Eje Temático: II. Geometría.
CMO: Area y Volumen de Cuerpos.
NEM: Cuarto Medio.
Eje Temático: II. Geometría.
CMO: Area y Volumen de Cuerpos.
Desafío - Volumen Pirámide
Una Pirámide de base cuadrada -cuyo lado mide 15 cm- posee una altura de 22 cm. ¿Cuánto mide su volumen ?
A) 220 cm cúbicos.
B) 330 cm cúbicos.
C) 660 cm cúbicos.
D) 1.650 cm cúbicos.
E) 4.950 cm cúbicos.
Respuesta:
Superficie de la base * Altura * 1/3
luego, en el caso concreto, aunque escrito en otro orden:
V = (1/3) (Superficie de Base) (Altura)
V = (1/3) (15x15) (22) centímetros Cúbicos.
V = 1.650 centímetros cúbicos.
Fuente: Guía CEPECH
NEM: Cuarto Medio.
Eje Temático: II. Geometría.
CMO: Area y Volumen de Cuerpos.
A) 220 cm cúbicos.
B) 330 cm cúbicos.
C) 660 cm cúbicos.
D) 1.650 cm cúbicos.
E) 4.950 cm cúbicos.
Respuesta:
La formula general para el volumen de una pirámide es:
luego, en el caso concreto, aunque escrito en otro orden:
V = (1/3) (Superficie de Base) (Altura)
V = (1/3) (15x15) (22) centímetros Cúbicos.
V = 1.650 centímetros cúbicos.
Fuente: Guía CEPECH
NEM: Cuarto Medio.
Eje Temático: II. Geometría.
CMO: Area y Volumen de Cuerpos.
Desafío - Área de Cubo
Respuesta:
Para determinar el área de un cubo, necesitamos saber su arista. El área de cubo mide:
Área de Cubo = 6 veces al área de una de sus caras (por que tiene 6 caras iguales)
Área de una cara = (arista) elevada al cuadrado.
Entonces, teniendo el valor de la arista estamos OK!
Cada una de las dos sentencias (1) y (2) me dan condiciones para tener la arista.
D) cada una por sí sola!
Fuente: Guía CEPECH
NEM: Cuarto Medio.
Eje Temático: II. Geometría.
CMO: Area y Volumen de Cuerpos.
Para determinar el área de un cubo, necesitamos saber su arista. El área de cubo mide:
Área de Cubo = 6 veces al área de una de sus caras (por que tiene 6 caras iguales)
Área de una cara = (arista) elevada al cuadrado.
Entonces, teniendo el valor de la arista estamos OK!
Cada una de las dos sentencias (1) y (2) me dan condiciones para tener la arista.
D) cada una por sí sola!
Fuente: Guía CEPECH
NEM: Cuarto Medio.
Eje Temático: II. Geometría.
CMO: Area y Volumen de Cuerpos.
Desafío - Volumen de Cono
Se puede determinar el volumen de un CONO (Pi, = 3,1415....) si:
(1) El perímetro de la base mide 12 pi cm
(2) La altura del cono mide 9 cm
A) (1) por sí sola.
B) (2) por sí sola.
C) Ambas Juntas, (1) y (2).
D) Cada una por sí sola, (1) ò (2)
E) Se requiere información adicional.
Respuesta:
Mira el Link donde está la fórmula del Volumen de Cono: Volumen de Cono
De acuerdo al Link, para el Volumen de Cono necesitamos:
1) el radio de la circunferencia basal.
2) la altura del cono.
Miremos (1): Con el perímetro de la base tenemos el radio.
Miremos (2): Nos dan directamente la altura.
Ambas Juntas (1) y (2) :
Alternativa C)
Fuente: Guía CEPECH
NEM: Cuarto Medio.
Eje Temático: II. Geometría.
CMO: Area y Volumen de Cuerpos.
(1) El perímetro de la base mide 12 pi cm
(2) La altura del cono mide 9 cm
A) (1) por sí sola.
B) (2) por sí sola.
C) Ambas Juntas, (1) y (2).
D) Cada una por sí sola, (1) ò (2)
E) Se requiere información adicional.
Respuesta:
Mira el Link donde está la fórmula del Volumen de Cono: Volumen de Cono
De acuerdo al Link, para el Volumen de Cono necesitamos:
1) el radio de la circunferencia basal.
2) la altura del cono.
Miremos (1): Con el perímetro de la base tenemos el radio.
Miremos (2): Nos dan directamente la altura.
Ambas Juntas (1) y (2) :
Alternativa C)
Fuente: Guía CEPECH
NEM: Cuarto Medio.
Eje Temático: II. Geometría.
CMO: Area y Volumen de Cuerpos.
Desafío - Volumen Esfera
Respuesta:
Alternativa D)
Fuente: Guía CEPECH
NEM: Cuarto Medio.
Eje Temático: II. Geometría.
CMO: Area y Volumen de Cuerpos.
Alternativa D)
Fuente: Guía CEPECH
NEM: Cuarto Medio.
Eje Temático: II. Geometría.
CMO: Area y Volumen de Cuerpos.
Desafío - Área de Cubo
Si la arista de un cubo mide 4 cm, entonces el área del cubo mide:
A) 12 cm cuadrados.
B) 48 cm cuadrados.
C) 64 cm cuadrados.
D) 96 cm cuadrados
E) 576 cm cuadrados.
Respuesta: El Área de un cubo mide 6 veces el área de una de sus caras (son 6 caras iguales) y cada cara es un cuadrado, por tanto su área es el cuadrado de la arista ....
Área Total de un cubo = 6 (4 cm) (4 cm) = 96 cm cuadrados.
Alternativa D)
Fuente: Guía CEPECH
NEM: Cuarto Medio.
Eje Temático: II. Geometría.
CMO: Area y Volumen de Cuerpos.
A) 12 cm cuadrados.
B) 48 cm cuadrados.
C) 64 cm cuadrados.
D) 96 cm cuadrados
E) 576 cm cuadrados.
Respuesta: El Área de un cubo mide 6 veces el área de una de sus caras (son 6 caras iguales) y cada cara es un cuadrado, por tanto su área es el cuadrado de la arista ....
Área Total de un cubo = 6 (4 cm) (4 cm) = 96 cm cuadrados.
Alternativa D)
Fuente: Guía CEPECH
NEM: Cuarto Medio.
Eje Temático: II. Geometría.
CMO: Area y Volumen de Cuerpos.
Desafío - Volumen
Si la arista de un cubo mide 2 cm, entonces el doble del volumen del cubo mide = ?
A) 16 cm cúbicos
B) 12 cm cúbicos
C) 8 cm cúbicos
D) 6 cm cúbicos
E) Ninguna de las anteriores
Respuesta:
Volumen = (2 cm)(2 cm)(2 cm) = 8 cm cúbicos.
Luego, el
doble del Volumen del cubo es = 2x(8 cm cúbicos)
= 16 cm cúbicos
Alternativa A)
Fuente: Guía CEPECH
NEM: Cuarto Medio.
Eje Temático: II. Geometría.
CMO: Area y Volumen de Cuerpos.
A) 16 cm cúbicos
B) 12 cm cúbicos
C) 8 cm cúbicos
D) 6 cm cúbicos
E) Ninguna de las anteriores
Respuesta:
Volumen = (2 cm)(2 cm)(2 cm) = 8 cm cúbicos.
Luego, el
doble del Volumen del cubo es = 2x(8 cm cúbicos)
= 16 cm cúbicos
Alternativa A)
Fuente: Guía CEPECH
NEM: Cuarto Medio.
Eje Temático: II. Geometría.
CMO: Area y Volumen de Cuerpos.
Desafío - Volumen
La razón entre las áreas de dos cubos es 9:16.
¿ Cuál es la razón entre sus volúmenes ?
A) 729:4096
B) 27:64
C) 9:16
D) 9:12
E) 3:4
Respuesta:
Sea que el cubo chico tiene lado "a" y que el cubo GRANDE tiene lado "A".
Luego podemos establecer:
Fuente: Guía CEPECH
NEM: Cuarto Medio.
Eje Temático: II. Geometría.
CMO: Area y Volumen de Cuerpos.
¿ Cuál es la razón entre sus volúmenes ?
A) 729:4096
B) 27:64
C) 9:16
D) 9:12
E) 3:4
Respuesta:
Sea que el cubo chico tiene lado "a" y que el cubo GRANDE tiene lado "A".
Luego podemos establecer:
Alternativa B)
Fuente: Guía CEPECH
NEM: Cuarto Medio.
Eje Temático: II. Geometría.
CMO: Area y Volumen de Cuerpos.
Desafío - Volumen
El volumen de un cubo es 729 cm cúbicos. ¿Cuál(es) de las siguientes afirmaciones es(son) verdadera(s)?
A) Sólo I
B) Sólo II
C) Sólo I y II
D) Sólo I y III
E) I, II, III
Respuesta: Si el volumen del cubo es 729 cm cúbicos, entonces la arista del cuco es (raíz cúbica de 729) = 9 cm.
y de acuerdo al siguiente esquema:
I) VERDADERA: La diagonal de una cara es 9 x (raíz de 2)
II) FALSA: El área del cubo es 6 x (81) cm cuadrados.
III) VERDADERA: La diagonal del cubo es 9 x (raíz de 3)
I y III verdaderas: Alternativa D)
Fuente: Guía CEPECH
NEM: Cuarto Medio.
Eje Temático: II. Geometría.
CMO: Area y Volumen de Cuerpos.
A) Sólo I
B) Sólo II
C) Sólo I y II
D) Sólo I y III
E) I, II, III
Respuesta: Si el volumen del cubo es 729 cm cúbicos, entonces la arista del cuco es (raíz cúbica de 729) = 9 cm.
y de acuerdo al siguiente esquema:
I) VERDADERA: La diagonal de una cara es 9 x (raíz de 2)
II) FALSA: El área del cubo es 6 x (81) cm cuadrados.
III) VERDADERA: La diagonal del cubo es 9 x (raíz de 3)
I y III verdaderas: Alternativa D)
Fuente: Guía CEPECH
NEM: Cuarto Medio.
Eje Temático: II. Geometría.
CMO: Area y Volumen de Cuerpos.
Desafío - Área de Paralelepípedo
Si un paralelepípedo mide 8 cm de largo, 6 cm de ancho y 3 cm de alto, entonces su área total mide:
A) 84 cm cuadrados.
B) 90 cm cuadrados.
C) 180 cm cuadrados.
D) 510 cm cuadrados.
E) 1.020 cm cuadrados.
Respuesta:
Si las aristas del parelelepípedo miden a, b, c, entonces
El Área Total = 2(ab+bc+ac)
En nuestros caso (aunque puede ser otro el orden de las letras):
a = 8
b = 6
c = 3
El Área Total = 2( 8x6 + 6x3 + 8x3 )
El Área Total = 2(48 + 18 + 24 )
El Área Total = 2(90)
El Área Total = 180 cm cuadrados
Alternativa C)
Fuente: Guía CEPECH
NEM: Cuarto Medio.
Eje Temático: II. Geometría.
CMO: Area y Volumen de Cuerpos.
A) 84 cm cuadrados.
B) 90 cm cuadrados.
C) 180 cm cuadrados.
D) 510 cm cuadrados.
E) 1.020 cm cuadrados.
Respuesta:
Si las aristas del parelelepípedo miden a, b, c, entonces
El Área Total = 2(ab+bc+ac)
En nuestros caso (aunque puede ser otro el orden de las letras):
a = 8
b = 6
c = 3
El Área Total = 2( 8x6 + 6x3 + 8x3 )
El Área Total = 2(48 + 18 + 24 )
El Área Total = 2(90)
El Área Total = 180 cm cuadrados
Alternativa C)
Fuente: Guía CEPECH
NEM: Cuarto Medio.
Eje Temático: II. Geometría.
CMO: Area y Volumen de Cuerpos.
Desafío - Volumen
Respuesta: Para la altura tendremos que usar pitágoras, porque tenemos la hipotenusa (6) y el cateto (3), veamos:
Fuente: Guía CEPECH
NEM: Cuarto Medio.
Eje Temático: II. Geometría.
CMO: Area y Volumen de Cuerpos.
Desafío - Volumen
Si el radio de una esfera mide 9 cm, entonces su área mide = ?
Respuesta:
Ver el Link: Volumen y Área de Esfera
o mejor, mirar directamente la siguiente imagen de la WEB:
Luego, calculamos, usando la fórmula:
Alternativa E)
Fuente: Guía CEPECH
NEM: Cuarto Medio.
Eje Temático: II. Geometría.
CMO: Area y Volumen de Cuerpos.
Respuesta:
Ver el Link: Volumen y Área de Esfera
o mejor, mirar directamente la siguiente imagen de la WEB:
Luego, calculamos, usando la fórmula:
Alternativa E)
Fuente: Guía CEPECH
NEM: Cuarto Medio.
Eje Temático: II. Geometría.
CMO: Area y Volumen de Cuerpos.
jueves, 5 de abril de 2012
Desafío - Exponenciales
Respuesta:
Alternativa B)
Fuente: PreU P. valdivia.
NEM: Cuarto Medio.
Eje Temático: I) Álgebra y Funciones.
CMO: Ecuaciones Exponenciales.
Alternativa B)
Fuente: PreU P. valdivia.
NEM: Cuarto Medio.
Eje Temático: I) Álgebra y Funciones.
CMO: Ecuaciones Exponenciales.
miércoles, 4 de abril de 2012
Desafío - Proporcionalidad en Circunferencia
En la figura,
QP = 2PC, AP=4cm, QP+NB=6cm, AB=2NB
y O es el centro de la circunferencia.
Entonces BM=?
A) 5cm
B) 7 cm
C) 4 cm
D) 6 cm
E) 8 cm
Respuesta:
Fuente: Selección Ejercicios Profesor Campillai
NEM: Segundo Medio.
Eje Temático: II. Geometría.
CMO: Proporcionalidad en la circunferencia.
QP = 2PC, AP=4cm, QP+NB=6cm, AB=2NB
y O es el centro de la circunferencia.
Entonces BM=?
A) 5cm
B) 7 cm
C) 4 cm
D) 6 cm
E) 8 cm
Respuesta:
Fuente: Selección Ejercicios Profesor Campillai
NEM: Segundo Medio.
Eje Temático: II. Geometría.
CMO: Proporcionalidad en la circunferencia.