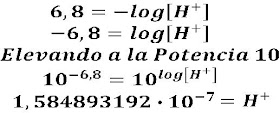Respuesta:
Alternativa D)
Fuente: Faccímil 500 problemas PSU Matemáticas.
NEM: Segundo Medio.
Eje Temático: II. Geometría.
CMO: Sección Áurea.













 Respuesta: Por la propiedad de las raíces, todas las raíces se pueden multiplicar en índices y se transforman en raíces de índice 60.
Respuesta: Por la propiedad de las raíces, todas las raíces se pueden multiplicar en índices y se transforman en raíces de índice 60.
 El cuociente entre la mayor de la coordenadas y la menor, de la solución del sistema de ecuaciones anterior es:
El cuociente entre la mayor de la coordenadas y la menor, de la solución del sistema de ecuaciones anterior es: Respuesta:
Respuesta: Respuesta: Llamamos "x" al precio del artículo:
Respuesta: Llamamos "x" al precio del artículo: Respuesta: Descontar a un cliente un 10% equivale a venderle el producto en 90% del valor inicial.
Respuesta: Descontar a un cliente un 10% equivale a venderle el producto en 90% del valor inicial.  Respuesta: El porcentaje pedido es:
Respuesta: El porcentaje pedido es:





 Respuesta: Por el principio multiplicativo y sabiendo que cada uno de los dados tiene 6 números posibles, es que hay (6)(6)(6) = 216, resultados equiprobables. Sólo uno de ellos tiene un número 1 en el primer dado, un número 2 en el segundo dado y un número 3 en el tercer dado.
Respuesta: Por el principio multiplicativo y sabiendo que cada uno de los dados tiene 6 números posibles, es que hay (6)(6)(6) = 216, resultados equiprobables. Sólo uno de ellos tiene un número 1 en el primer dado, un número 2 en el segundo dado y un número 3 en el tercer dado. Respuesta:
Respuesta:






 Respuesta: Hagamos un plan:
Respuesta: Hagamos un plan: